Roinnt Gníomhartha Úsáideacha

Níos mó oibritheoirí

Chonaiceamar níos luaithe sa teagasc seo na hoibritheoirí +, -, * agus /. Tá dhá oibritheoirí matamaitice eile ag Setanta, an oibritheoir “modulo” (%) agus an oibritheoir roinnt-slánuimhreacha (//).

Modulo

Is oibritheoir neamhghnách é an oibritheoir modulo (%), ach tá sé an-úsáideach.

Glacann an oibritheoir sin le dhá uimhir, roinneann sé an chéad ceann ar an dara ceann agus tugann sé ar ais an fuílleach.

Mar shampla: tá 7 % 2 cothrom le 1 mar nuair a roinneann tú 7 le 2, tá an fuílleach cothrom le 1 (mar tá 7 == 3*2 + 1). Mar an gcéanna, tá 11 % 4 cothrom le 3 mar tá 11 == 2*4 + 3.

Corr nó Réidh?

Tá an oibritheoir seo úsáideach mar is féidir linn é a úsáid chun a lán rudaí a dhéanamh. Mar shampla: is féidir linn é a úsáid chun seiceáil an bhfuil uimhir éigin corr nó réidh. Chun é sin a dhéanamh níl ach le déanamh againn ach seiceáil cad é an fuílleach nuair a roinneann tú an uimhir ar 2. Má tá an fuílleach cothrom le 0, is uimhir réidh é mar is féidir linn an uimhir a roinnt ar 2 gan fuílleach. Má tá sé cothrom le 1 is uimhir corr é. Bain triail as an ríomhchlár seo:

An bhfuil sé príomha?

Is féidir linn an oibritheoir modulo % a úsáid chun seic a dhéanamh an féidir leat uimhir a roinnt faoi uimhir eile (má tá x % y == 0, is féidir leat x a roinnt ar y). Is féidir linn an cumas seo a úsáid chun seiceáil an bhfuil uimhir éigin príomha.

Is uimhir príomha é uimhir lé 2 fhachtóir, an uimhir féin agus 1. Chun seic a dhéanamh an bhfuil uimhir príomha is féidir linn an méid fachtóirí a chomhaireamh mar seo:

gníomh príomha(x) {
    >-- Athróg don méid fachtóirí
    fachtóirí := 0

    >-- Déan seic ar gach uimhir idir 1 agus x
    le i idir (1, x + 1) {
        >-- Má tá an seic seo fíor, is féidir leat roinn x ar i.
        >-- Mar sin is fachtóir é i.
        má x % i == 0 {
            fachtóirí += 1
        }
    }

    >-- Má tá fachtóirí == 2, is uimhir príomha é x.
    >-- Mura bhfuil sé, ní uimhir príomha é x.
    toradh fachtóirí == 2
}

Bain triail as an cód sin le cúpla uimhir:

NB: Tá algartaim níos fearr ná seo, an féidir leat é a chruthú? Ní gá dúinn seic an bhfuil 1 nó x ina fhachtóir mar tá beidh fuílleach 0 ann i gcónaí, ach aisteach go leor, ní gá dúinn seic a dhéanamh ar aon uimhir níos mó ná √x, cén fáth?

Liostaí gan teorainn

Léigh an ríomhchlár seo agus smaoinigh faoin seicheamh uimhreacha a scríobhann sé.

Scríobhann an ríomhchlár sin fuílleach gach uimhir idir 0 agus 15 nuair a roinneann tú iad ar 5. Má léann tú an seicheamh uimhreacha a scríobhann sé feicfidh tú an seicheamh “0”, “1”, “2”, “3”, “4”, ansin tosaíonn sé ar ais ag “0” agus leanann sé ar aghaidh sa treo céanna: “1”, “2”, “3” “4”, “0” … srl.

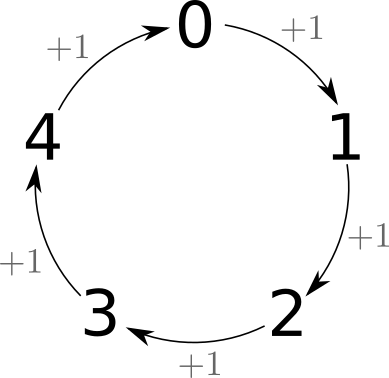
Má ritheann tú an ríomhchlár sin le raon uimhreacha níos mó feicfidh tú an patrún céanna. Níl tharlaíonn an patrún sin le i % 5 amháin, má dhéanann tú an rud céanna le uimhir éigin n, gheobhaidh tú an seicheamh 0, 1, 2 ... n - 1, 0, 1, 2, ..., n - 1, ... srl.

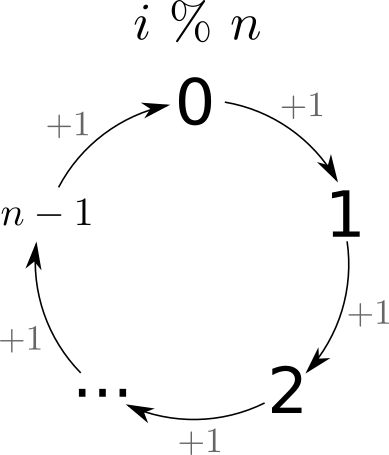
Is féidir linn an patrún seo a úsáid chun dul thar liosta arís agus arís, cosúil go liosta gan teorainn é:

Féach ar gcód seo:

Scríobhann an ríomhchlár sin baill an liosta ach ansin baineann sé triail an ball ag an innéacs 3 a roghnú agus teipeann air mar tá 3 ró mhór. Ach, má úsáidimid an oibritheoir modulo % chun dul ar ais go 0 nuair a shroichimid deireadh an liosta beidh gach rud ceart go leor. Tá fad an liosta cothrom le 3, dá bhrí sin beidh i % fad@liosta cothrom le 0, 1 nó 2 i gcónaí. Bain triail as ár gcód nua:

Anois ní theipeann ar an ríomhchlár nuair a shroicheann sé deireadh an liosta, in ionad sin téann sé ar ais go dtí an tús. Bain triail as teanga nua a chuir leis an liosta agus an cód a rith arís, feicfidh tú go dhéanann sé an rud céanna: rachaidh an lúb thar an liosta arís agus arís.

Gníomhartha Matamaitice

Chonaiceamar roinnt gníomhartha matamaitice cheanna sa teagasc seo, go háirithe rand@mata agus slánuimh_rand@mata, áfach, tá i bhfad níos mó gníomhartha agus luachanna matamaitice ar fáil i Setanta.

Seo liosta gearr do na gníomhartha agus luachanna atá ar fáil, bá chóir duit @mata a úsáid chun iad a roghnú, mar shampla fréamh@mata.

go_téacs

Is féidir linn go_téacs a úsáid chun aon luach a athrú go léiriú téacsúil. Mar shampla: is ionann go_téacs([1, 2, 3]) agus "[1, 2, 3]" agus is ionann go_téacs(scríobh) agus "<gníomh scríobh>".

Athchuir

Is féidir linn an gníomh athchuir a úsáid chun cuid den píosa téacs a athrú go píosaí téacs eile. Mar shampla ba féidir linn aghaidh shona “:)” a chuir i bpíosa téacs in ionad gach aghaidh brónach “:(”.

Cuimhnigh anois caithfimid “@” a úsáid le píosa téacs chun fad an píosa a téacs a fháil mar seo: fad@"Sligeach". Sa chaoi chéanna, caithfimid “@” a úsáid chun athchuir a úsáid.

Seo cúpla sampla conas athchuir a úsáid:

Roinn

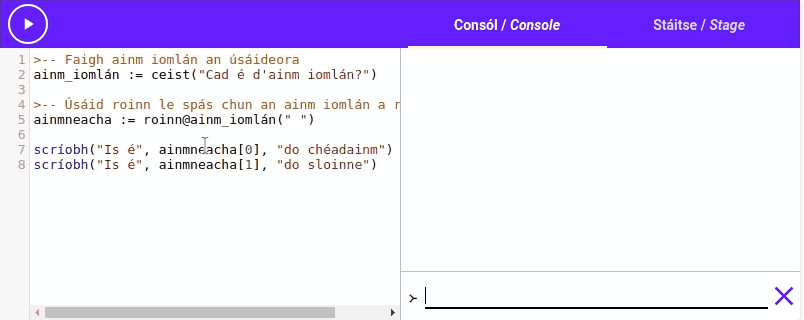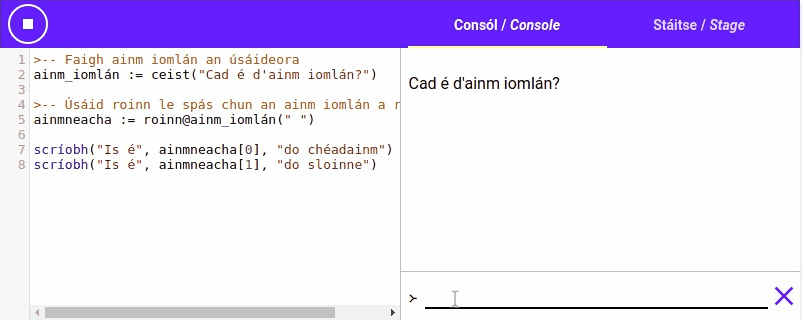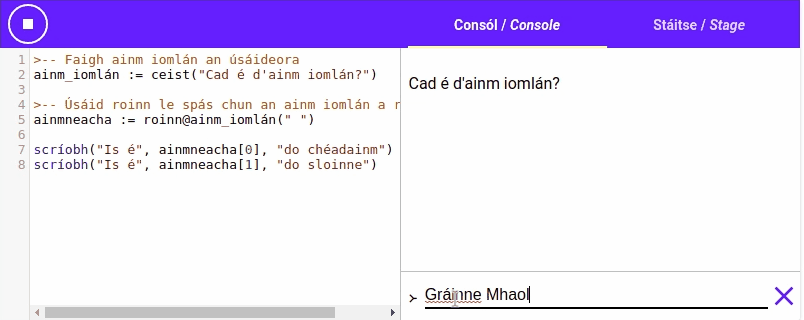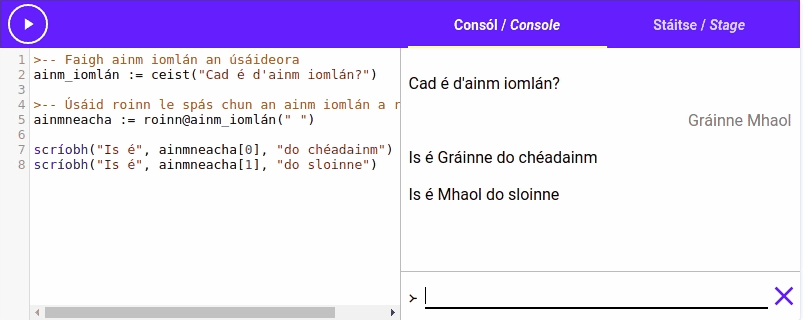
Is féidir linn an gníomh roinn a úsáid chun píosa téacs a roinnt i fo-píosaí. Is féidir linn carachtar éigin a roghnú agus nuair a glaoimid ar roinn leis an gcarachtar, faighimid ar ais liosta le gach cuid den píosa téacs atá scartha óna gcéile ag an gcarachtar sin.

Mar shampla: is féidir linn roinn a úsáid le camóg (“,”) chun píosa téacs cosúil le "Setanta,Python,Java" a roinnt agus an liosta ["Setanta", "Python", "Java"] a fháil. Is féidir linn roinn a úsáid le spás (" ") chun abairt éigin a roinnt ina fhocail ar leith.

Bain triail as an ríomhchlár seo:

Cuid

Leis an gníomh cuid, is féidir linn cuid a bhaint amach as píosa téacs. Glacann an gníomh le 2 innéacs mar argóintí agus tugann sé an fo-píosa téacs idir na innéacs sin. (Cuimsíonn sé an chéad innéacs, ach ní chuimsíonn sé an dara cheann).

Mar shampla: Tá cuid@"Setanta"(1, 4) cothrom le "eta" mar is é “eta” an téacs idir an innéacs 1 agus 4 i “Setanta”. (Setanta).

go_liosta

Glacann an gníomh go_liosta le píosa téacs, agus tugann sé liosta ar ais le gach carachtar ón bpíosa téacs ar leith. Mar shampla: Tá go_liosta("Setanta") cothrom le ["S", "e", "t", "a", "n", "t", "a"].

Sórtáil

Is féidir an gníomh sórtáil a úsáid chun liosta a sórtáil ( mar a shamhlófá). Cuireann sórtáil an liosta in ord méadaitheach. Mar shampla tá sórtáil@[1, 3, 2] cothrom le [1, 2, 3].

NB: Tugann sórtáil an liosta sórtáilte ar ais, ach athráionn sé an liosta freisin. Ní cruthaíonn sé liosta nua: athráíonn sé ord an liosta go díreach.

Nasc

Déanann an gníomh nasc an rud contrártha leis an ngníomh roinn. Cruthaíonn sé píosa téacs ó liosta. Glacann sé le carachtar éigin agus cruthaíonn sé píosa téacs ó liosta, leis an gcarachtar sin idir gach ball den liosta.

Mar shampla: Is é "1, 2, 3" an toradh ar nasc@[1, 2, 3](", ").