Some Useful Actions

More Operators

Setanta has 2 more operators that we haven’t seen yet. They are the “modulo” operator (%), and the integer division operator (//).

Modulo

The modulo operator (%) is an operator you might not be familiar with, but it’s extremely useful.

The modulo operator takes two numbers, and returns the remainder when one is divided by the other.

e.g. 7 % 2 is equal to 1, because 7 has remainder 1 when divided by 2. 11 % 4 has remainder 3, because 11 has remainder 3 when divided by 4.

This operator is extremely useful because it allows us to check lots of things.

Odd or Even?

For example, we can check if a number is odd or even by checking if has remainder 1 or 0 when divided by 2. Try it out here!

Is it prime?

We can also use % to check if one number is divisible by another. A number is divisible by another number if it leaves 0 remainder when you divide by it. e.g. 10 % 2 and 10 % 5 are both 0 because 10 is divisible by 2 and 5.

We can use this to check if a number is prime! A prime number will have exactly 2 divisors.

>-- Action to check is `x` prime
gníomh is_prime(x) {
    >-- Variable to count divisors
    divisors := 0

    >-- Check all numbers from 1 to x
    le i idir (1, x + 1) {
        >-- If x % i == 0 then i is a divisor
        má x % i == 0 {
            >-- Add 1 to divisor count
            divisors += 1
        }
    }

    >-- If divisors == 2, then x is prime
    >-- If divisors isn't 2, then x not prime
    toradh divisors == 2
}

Let’s try it out! Run this code and try some primes and non-primes:

NB: There is a better algorithm than this, can you create it? We don’t have to check if 1 or x are factors because they always have remainder 0, but actually we don’t have to check any number greater than √x, why?

Infinite lists

Read this program and think about the list of numbers it writes.

This program writes the remainder of every number between 0 and 15 after division by 5. If you read the sequence of numbers it writes you’ll see the sequence “0”, “1”, “2”, “3”, “4”, and then it starts again at “0” and continues in the same way: “1”, “2”, “3”, “4”, “0” … etc.

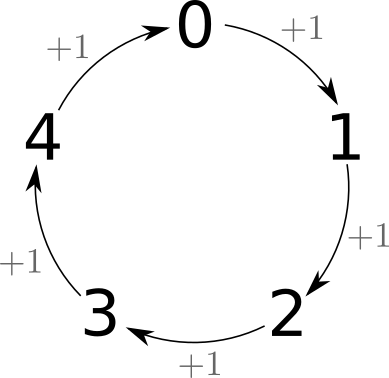
If you run that program with a bigger range of numbers, you’ll see the same pattern. This pattern doesn’t only happen with i % 5, if you do the same thing with some number n you’ll get the sequence 0, 1, 2 ... n - 1, 0, 1, 2, ..., n - 1, ... etc.

We can use this pattern to go through a list again and again, as if it was infinite.

Look at this code:

That program write the members of the list, but then it tries to the member at index 4 and it fails because 4 is too big. But, if we use the modulo operator % to go back around to 0 when we reach the end of the list everything will be ok. The length of the list is equal to 3 so i % fad@list will always be equal to 0, 1 or 2. Try out our new code:

Now the program doesn’t fail when it gets to the end of the list, instead it goes back to the start. Try adding a new language to the list and run the code again, you’ll see that it does the same thing, it goes through the list again and again.

Maths actions

Earlier in the tutorial we got lots of use out of rand@mata and slánuimh_rand@mata to get random numbers. However, those are not the only maths actions we have.

Here is a quick list of actions and values you can access: Don’t worry if you don’t know what some of the actions do. They’re available for anyone who needs them.

go_téacs / To Text

Use go_téacs to convert any value to a text representation. “go téacs” translates as “to text”.

For example go_téacs([1, 2, 3]) == "[1, 2, 3]" and go_téacs(scríobh) == "< gníomh scríobh >"

Athchuir / Replace

Athchuir translates as “replace”. You can use the athchuir action to replace parts of text with another piece of text. For example you could replace every sad face (“:(”) in a piece of text with a happy face (“:)”).

If you remember how we had to use the @ symbol to use fad to get the length of the text (fad@"hey" == 3), we also have to use the @ symbol to use athchuir.

Check out some examples:

Roinn / Split

“Roinn” means “split” or “divide”. We can use the roinn action to split up a piece of text at certain points. For example we could use roinn with commas to divide up a comma separated list like "Setanta, is, fun" into the list ["Setanta", "is", "fun"]. Or we could use roinn with spaces to separate a sentence into a list of words.

Try it out:

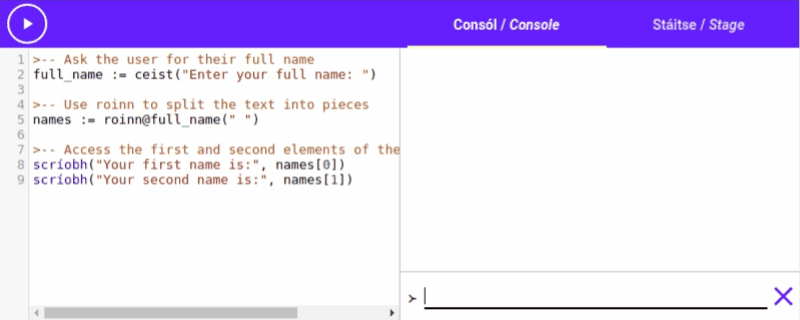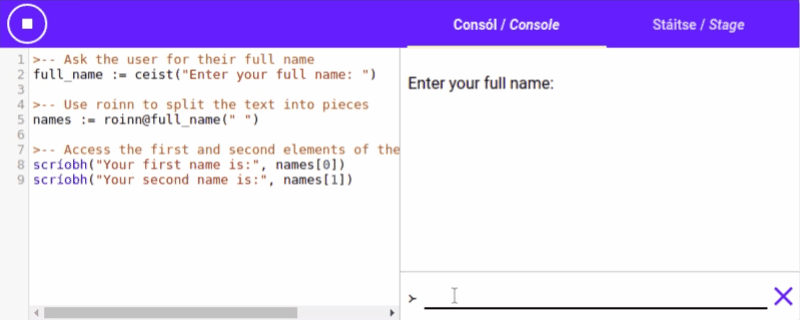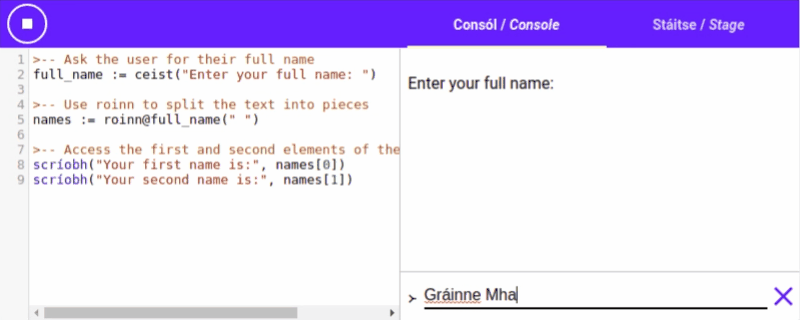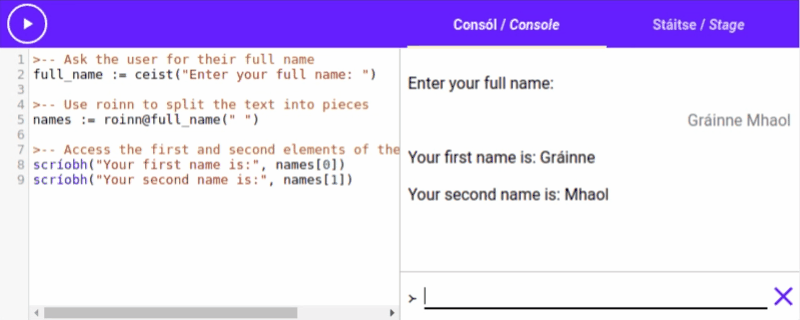
Cuid / Part

“Cuid” means “part” or “piece”, and the cuid action allows us to extract a piece of text. We give the action 2 positions as arguments, and it returns the text between those 2 positions (not including the second).

e.g. cuid@"hello"(1, 4) returns "ell" because the text between index 1 and index 4 is "ell"

go_liosta/ To List

go_liosta (meaning “to list”) is an action that returns a list of the characters of the text.

e.g. go_liosta("Setanta") returns ["S", "e", "t", "a", "n", "t", "a"].

Sórtáil / Sort

“Sórtaíl” translates as “sort”, the sórtáil action sorts a list into increasing order.

For example: sórtáil@[1, 3, 2] returns [1, 2, 3].

NB: Sorting is done in place. i.e. the list will be changed when sórtáil is called

Nasc / Join

“Nasc” translates as “join”. The nasc action can be used to turn a list into text, joining the elements together with some piece of text. This text is passed in as an argument.

For example: nasc@[1, 2, 3](", ") returns "1, 2, 3"